The Chacon function below is an implementation of the Chacon transformation of the unit interval \((0,1)\). The definition of the Chacon transformation can be found in this thesis.

Chacon <- function(x){ 
  n <- 1L
  while(3L^(n+1L)*x >= 3L^(n+1L) - 1L) n <- n+1L 
  while(3L^(n+1L)*x >= 2L*3L^n - 2L && 3L*x < 2L) n <- n+1L
  i <- 1L; A <- c(0L, 2L, 6L, 4L)/9L
  if((3^(n+1)-1)/2 > 2^31-1) stop("there's a too long vector")
  while(i < n){
    A <- c(A, A + 2L/3L^(i+2L), 1L - 1L/3L^(i+1L), A + 4L/3L^(i+2L))
    i <- i+1L
  }
  dists <- x-A
  j <- which(dists >= 0 & 3L^(n+1L)*dists < 2)
  return(A[j+1L]+dists[j]) 
}

Below is a plot of the Chacon transformation.

par(mar=c(4,4,0,0))
u <- seq(0, 0.995, by=.005) 
Cu <- sapply(u, Chacon)
plot(u, Cu, pch=19, cex=0.2, asp=1, xlim=c(0,1), pty="s")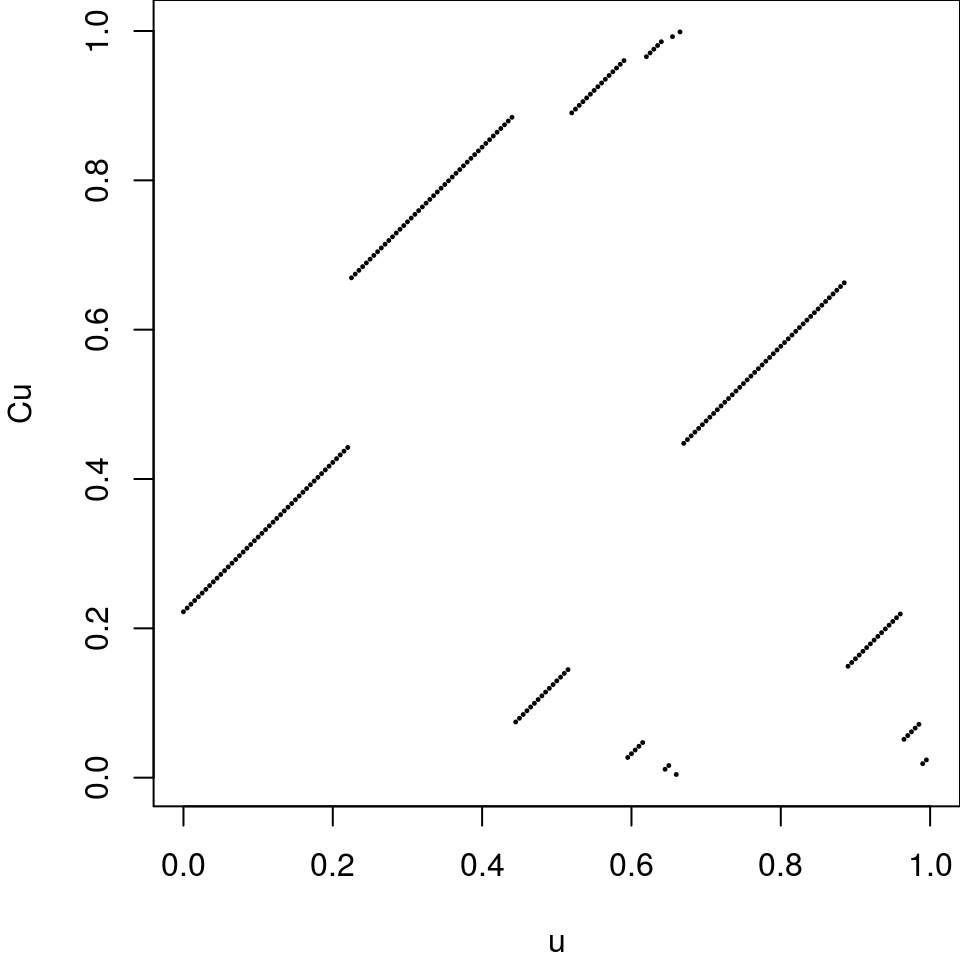

This is probably rather useless.