-
Entropie d'une mesure discrète de masse infinie
04/10/2015
Source(latest update : 2015-10-05 21:42:25)
Les investigations du présent article prennent leurs origines dans mon article [2], et sont motivées par la détermination de l’entropie de la filtration du processus du prochain saut, à laquelle je n’ai pas encore réussi à parvenir. Bien que cela soit motivé par un problème d’entropie dans le cadre de la théorie des filtrations à temps discret négatif, le présent article ne met aucunement en jeu les filtrations et concerne uniquement des faits sur l’entropie des variables aléatoires discrètes, qui sont intéressants en eux-mêmes.
Nous donnerons en particulier un critère de comparaison entre les entropies de deux variables aléatoires sur \(\mathbb{N}\) ainsi qu’un critère de monotonie en \(n\) de l’entropie de la loi d’une variable aléatoire sur \(\mathbb{N}\) conditionnée à \(\{0, \ldots, n\}\). Bien qu’élémentaires, je n’ai trouvé ces critères nulle part dans la littérature.
Les \(p_n\) d’une loi discrète
À travers tout l’article, nous ne considérons que des variables aléatoires (ou des probabilités) dont le support est \(\mathbb{N}\) ou bien \(\{0, \ldots, N\}\), hormis dans la dernière partie où nous considérerons aussi des mesures sur \(\mathbb{N}\) pas nécessairement normalisables. Afin d’unifier les deux cas nous disons alors que le support \(\{0, \ldots, N\}\) en autorisant \(N=\infty\).
Étant donnée une telle variable aléatoire \(X\), on note \(p_n=\Pr(X=n \mid X \leq n)\) pour tout \(n\) dans le support de \(X\). Notez que \(p_0=1\). Les \(p_n\) déterminent la loi de \(X\) de façon unique. En effet, on obtient après un peu de gymnastique \[ \frac{\Pr(X=k)}{\Pr(X=0)} = \frac{p_k}{(1-p_{1})\cdots(1-p_k)} \] ainsi que \[ \frac{\Pr(X\leq k)}{\Pr(X=0)} = \frac{1}{(1-p_{1})\cdots(1-p_k)}, \] et il vient alors \[ \Pr(X \leq k) = (1-p_N)\cdots(1-p_{k+1}) \] et \[ \Pr(X=k) = (1-p_N)\cdots(1-p_{k+1})p_{k}, \] où il s’agit d’un produit convergent lorsque \(N=\infty\). Notez que cette convergence se traduit par \(\boxed{\sum p_n < \infty}\).
Notez que \(p_n=\frac{1}{n+1}\) pour la loi uniforme sur \(\{0, \ldots N\}\).
Représentation intégrale de l’entropie
L’entropie de la variable aléatoire \(X\) admet la représentation suivante \[ \boxed{H(X) = \mathbb{E}\left[\dfrac{h(p_X)}{p_X}\right]} \] où \(h(p) = -p\log p - (1-p) \log(1-p)\) est l’entropie d’une épreuve de Bernoulli de probabilité de succès \(p\). Je n’ai pas essayé d’établir cette formule directement à l’aide des formules précédentes ; il n’y a pas de raison que ce ne soit pas possible, mais nous la verrons apparaître plus tard sans faire de calcul rébarbatif, à partir d’une relation de récurrence.
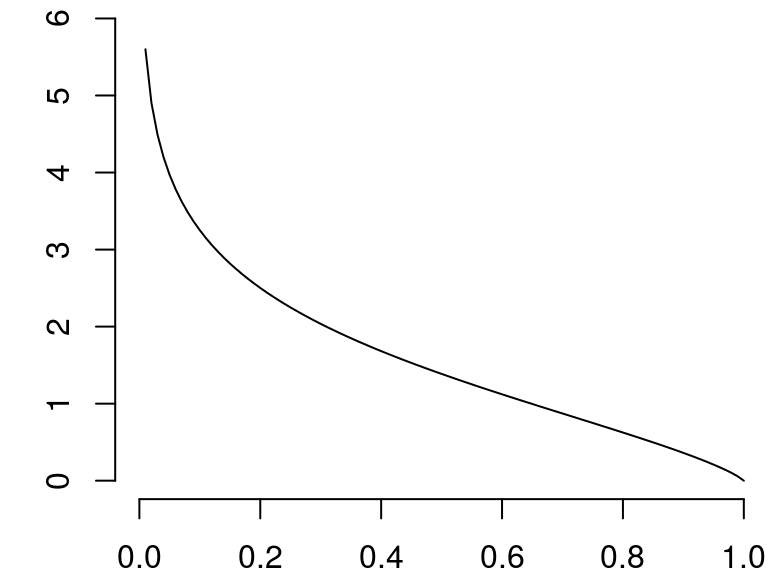
Remarquez que la fonction \(x \mapsto h(x)/x\) est décroissante :
Représentation probabiliste
Donnons-nous des \(p_n\), avec \(p_0=1\). Considérons une suite de variables de Bernoulli indépendantes \({(\epsilon_k)}_{k \geq 0}\) telles que \(p_k=\Pr(\epsilon_k=1)\). En particulier, \(\epsilon_0=0\), ce qui permet de définir la variable aléatoire
\[X_N = \max\bigl\{ k\in\{0, \ldots, N\} \mid \epsilon_k=1 \bigr\}.\] Notez que \(X_N\) est bien définie dans le cas \(N=\infty\) en vertu du premier lemme de Borel-Cantelli.La loi de la variable \(X_N\) ainsi définie est alors la même que celle de la variable aléatoire que nous avons aussi noté \(X\) auparavant. On peut aussi définir, pout tout \(n \in\{0, \ldots, N\}\), \[\boxed{X_n = \max\bigl\{ k\in\{0, \ldots, n\} \mid \epsilon_k=1 \bigr\}}.\] Il est facile de voir que “le \(p_k\)” de la loi conditionnelle de \(X_N\) sachant \(X_N \leq n\) n’est autre que le \(p_k\) de \(X_N\). Ainsi, la loi de \(X_n\) est la loi conditionnelle de \(X_N\) sachant \(X_N \leq n\). On a donc la loi de \(X_n\) qui s’exprime ainsi à l’aide des \(p_n\) : \[ \Pr(X_n \leq k) = (1-p_n)\cdots(1-p_{k+1}) \] et \[ \Pr(X_n=k) = (1-p_n)\cdots(1-p_{k+1})p_{k}. \]
Notez que la suite de variables aléatoires \(X_n\) est évidemment croissante en \(n\).
Entropie résiduelle
Reprenons des \(p_n\), avec \(p_0=1\), et considérons la variable aléatoire \(X\) associée, ainsi que les variables aléatoires \(X_n\), \(0 \leq n \leq N\), de la représentation probabiliste.
Notons \(\boxed{g_X(n) = H(X_n) = H(X \mid X \leq n)}\). Dans le cas \(N=\infty\), on a \(g_X(n) \to H(X)\), ceci résultant simplement du fait que \(\Pr(X \leq n) \to 1\).
Par la représentation intégrale de l’entropie, \[g_X(n) = \mathbb{E}\left[\frac{h(p_{X_n})}{p_{X_n}}\right].%=\mathbb{E}\left[\frac{h(p_{X_n})}{p_{X_n}}{\boldsymbol 1}_{\{X_n>0\}}\right].\]
J’ai précédemment promis de démontrer cette formule à l’aide d’une relation de récurrence. Cette relation est \[H(X_{n+1}) = h(p_{n+1}) + (1-p_{n+1})H(X_n), \] et elle découle de l’égalité \[H(X_n) + H(X_{n+1} \mid X_n) = H(X_{n+1}) + H(X_{n} \mid X_{n+1}) \] (les deux membres sont égaux à \(H(X_n,X_{n+1})\)), et de \[H(X_{n+1} \mid X_n) = h(p_{n+1}) \qquad \text{ et} \qquad H(X_{n} \mid X_{n+1}) = p_{n+1}H(X_n). \] De cette relation de récurrence, il vient facilement \[ H(X_n) = h(p_n) + (1-p_n)h(p_{n-1}) + (1-p_n)(1-p_{n-1})h(p_{n-2}) + \cdots + (1-p_n)\cdots(1-p_{2})h(p_{1}), \] et on obtient cette même expression lorsqu’on développe l’espérance dans la représentation intégrale.
En fait, je n’utilise vraiment les \(X_n\) que pour établir cette relation de récurrence. Ailleurs, j’utilise uniquement la loi de \(X_n\), et le fait qu’elle est stochastiquement croissante en \(n\).
Le théorème suivant résulte aisément du fait que la fonction \(x \mapsto h(x)/x\) est décroissante que \(X_n\) est croissant en \(n\).
Théorème. Si les \(p_n\) sont décroissants en \(n\), alors \(g_X(n)\) est croissant en \(n\).
Question. Est-ce que le cas croissant est vrai ? (Si, lorsqu’on ne tient pas compte de \(p_0\), les \(p_n\) sont croissants, alors \(g_X(n)\) est décroissant ?)
Notons maintenant \(\boxed{h_X(n) = H(X \mid X \geq n)}\). La fonction \(h_X\) est appelé l’entropie résiduelle de \(X\) dans la publication [3]. On note aussi \(r_X(n)=\frac{\Pr(X=n)}{\Pr(X \geq n)}\). La fonction \(r_X\) est bien connue sous le nom de taux de défaillance de \(X\). Le théorème suivant est démontré dans [3] pour les distributions à densité :
Théorème. Si \(r_X(n)\) est croissant en \(n\), alors \(h_X(n)\) est décroissant en \(n\).
Preuve: Supposons en un premier temps que \(N<\infty\) et posons \(Y_N=N-X_N\). On a alors \(\frac{\Pr(Y_N=n)}{\Pr(Y_N \leq n)}=r_{X_N}(N-n)\). Par conséquent, d’après le théorème précédent, \(g_{Y_N}(n)\) est croissant si \(r_{X_N}\) est croissant, et on conclut du fait que \(g_{Y_N}(n)=h_X(N-n)\). Dans le cas \(N=\infty\), en prenant n’importe quel entier \(M \geq 1\), on a, pour tout \(n\leq M\), \[ r_{X_M}(n) = r_X(n) \frac{\Pr(X\geq n)}{\Pr(X\geq n)- \Pr(X>M)}, \] et donc \(r_{X_M}\) est croissant si \(r_X\) est croissant. En raisonnant comme précédemment avec \(Y_M:=M-X_M\), on obtient la décroissance de \(h_X(n)\) pour \(n \in \{0, \ldots M\}\).
Question. Est-ce que \(h_X(n)\) est croissant lorsque \(r_n\) est décroissant ? C’est démontré dans [3] pour les distributions à densité.
Entropie d’une mesure sur \(\mathbb{N}\)
Précédemment, dans le cas \(N=\infty\), la suite \((p_n)\) satisfaisait \(\sum p_n < \infty\), du fait que le produit infini \(\prod(1-p_n)\) apparait dans \(\Pr(X \leq k)\) ou \(\Pr(X=k)\). Mais on peut se donner une suite \((p_n)\) quelconque (sauf \(p_0=1\)), et construire les variables aléatoires \(X_n\) de la représentation probabiliste comme précedemment.
La loi de \(X_n\) est alors la troncature d’une mesure \(\mu\) sur \(\mathbb{N}\), donnée par \[\mu(n) = \frac{p_n}{\prod_{k=1}^n (1-p_k)} = \frac{\Pr(X_n=n)}{\Pr(X_n=0)} \] ou \[\mu(0:n) = \frac{1}{\prod_{k=1}^n (1-p_k)} = \frac{1}{\Pr(X_n=0)} \] Cette mesure \(\mu\) est normalisable si et seulement si \(\boxed{\sum p_n < \infty}\). Dans ce cas \(X_n\) converge en loi vers la version normalisée de \(\mu\). Dans l’autre cas, le lemme de Borel-Cantelli montre que \(X_n=n\) une infinité de fois et donc que \(X_n \to \infty\).
Réciproquement, à une mesure \(\mu\), on associe \(p_n = \dfrac{\mu(n)}{\mu(0:n)}\).
Les résultats sur l’entropie de \(X_n\) que nous avons vus dans le cas \(\mu(\mathbb{N}) < \infty\), sont exactement les mêmes.
Définition: normalisation d’entropie
Nous donnons une définition de l’entropie d’une mesure \(\mu\) supportée par $.
Définissons la \(\epsilon\)-entropie d’une variable aléatoire discrète \(Y\) par \[ H^\epsilon(Y) = \inf\bigl\{H(F) \mid \Pr(F \neq Y) < \epsilon\bigr\}, \] où la borne inférieure est prise sur les variables aléatoires \(F\) qui sont (discrètes et) \(\sigma(Y)\)-measurables. Lorsque \(Y\) ne prend qu’un nombre fini de valeurs, on peut évidemment remplacer \(\inf\) par \(\min\).
Maintenant, étant donnée une mesure \(\mu\) supportée par \(\mathbb{N}\), et étant donnée une fonction \(c\colon \mathbb{N} \to \mathbb{R}^+\), appelée normalisation de l’entropie, on définit \[ \boxed{h_c(\mu) := \limsup_{\epsilon \to 0} \limsup_{n \to \infty} \dfrac{H^\epsilon(X_n)}{c(n)}}, \] où \(X_n \sim \mu(\cdot \mid 0:n)\).
L’entropie \(h_c(\mu)\) est invariante par bijection de \(\mathbb{N}\) qui ne transforme qu’une partie finie de \(\mathbb{N}\).
On pourrait plus généralement donner une définition relative à des \(A_n \nearrow \mathbb{N}\) en prenant \(X_n \sim \mu(\cdot \mid A_n)\).
Sans altérer \(h_c(\mu)\), on peut remplacer la définition de la \(\epsilon\)-entropie \(H^\epsilon(Y)\) par \[\inf \left\{- \sum_{i \in B} \nu(i)\log\nu(i) - \nu(B^c)\log\nu(B^c)\right\} \] où \(\nu\) est la loi de \(Y\) et la borne inférieure est prise sur toutes les parties \(B\) de l’espace d’états de \(Y\) vérifiant \(\mu(B^c) < \epsilon\).
Définitions. Nous disons que la normalisation d’entropie \(c(n)\) est :
propre si \(h_c(\mu) \in ]0, \infty[\);
exacte si \(h_c(\mu)=1\);
dominante si \(h_c(\mu) < \infty\);
négligeante si \(h_c(\mu) = 0\).
La normalisation d’entropie \(c(n)=H(X_n)\) est évidemment dominante.
Définition. Nous disons que \(\mu\) est d’entropie pleine si la normalisation d’entropie \(c(n)=H(X_n)\) est exacte.
Condition suffisante pour qu’une mesure soit d’entropie pleine
Lemme 1. S’il existe \(K>0\) tel que, pour tout \(n\geq 1\), \[\max_{B \subset \{0, \ldots, n\}} \dfrac{H\bigl(\mu(\cdot \mid B)\bigr)}{H(X_n)} \leq K, \] alors \(\mu\) est d’entropie pleine.
Preuve. Soient \(n\geq 1\) et \(\epsilon \in (0,1/K)\). Soit \(B \subset \{0, \ldots, n\}\) qui atteint le minimum dans la définition alternative de \(H^\epsilon(X_n)\). On note \(\mu_n=\mu(\cdot \mid 0:n)\) la loi de \(X_n\). On a \[-\sum_{i \in B^c} \mu_n(i)\log\mu_n(i) = \mu_n(B^c)H\bigl(\mu(\cdot \mid B^c)\bigr) - \mu_n(B^c)\log\mu_n(B^c) < \epsilon H\bigl(\mu(\cdot \mid B^c)\bigr) - \epsilon\log\epsilon. \]
\[H^\epsilon(X_n) = -\sum_{i\in B} \mu_n(i)\log\mu_n(i) - \mu_n(B^c)\log\mu_n(B^c) \]
\[H(X_n) = -\sum_{i \in B} \mu_n(i)\log\mu_n(i) -\sum_{i \in B^c} \mu_n(i)\log\mu_n(i).\]
On obtient alors \[H(X_n) \leq H^\epsilon(X_n) + \epsilon H\bigl(\mu(\cdot \mid B^c)\bigr) - \epsilon\log\epsilon, \] donc \[H(X_n) \leq \frac{1}{1-K\epsilon}\left(H^\epsilon(X_n) -\epsilon\log\epsilon \right) \]
\[ \frac{H^\epsilon(X_n)}{H(X_n)} \leq 1 \leq \frac{1}{1-K\epsilon}\left(\frac{H^\epsilon(X_n)}{H(X_n)} - \frac{-\epsilon \log\epsilon}{H(X_n)}\right),\] et le lemme s’ensuit.
Lemme 2. Si les \(p_n\) sont décroissants, alors \[H(X_n) > -\log p_K \Pr(X_n >K) \] pour tout \(n > K\).
Preuve. On utilise l’inégalité \[\dfrac{h(x)}{x} > -\log x \]
Par la représentation intégrale de l’entropie, et du fait que les \(p_n\) sont décroissants,
\[H(X_n) = \mathbb{E}\left[\frac{h(p_{X_n})}{p_{X_n}}\right] > \dfrac{h(p_K)}{p_K}\Pr(X_n >K) > -\log p_K \Pr(X_n >K) \]Application des deux lemmes. Soit \(\mu\) une mesure supportée par $ telle que \(\mu(n)\) est croissant en \(n\), et pour laquelle les \(p_n\) sont décroissants et vérifient \(\log n = O(-\log p_n)\) (ou \(-\log p_n=\Omega(\log n)\)). Alors \(\mu\) est d’entropie pleine.
Preuve. Vérifions que la condition du Lemme 1 est satisfaite. On applique le Lemme 2 avec \(K=[n/2]\). Cela donne \(H(X_n) > -\frac{1}{2}\log p_{[n/2]}\), et on a alors \(H(X_n) = \Omega(\log n)\) par l’hypothèse \(\log n = O(\log p_n)\). Puisque \(H\bigl(\mu(\cdot \mid B)\bigr) \leq \log\#B \leq \log n\), la condition du Lemme 1 est satisfaite.
