Nous avons vu comment un qubit, à un facteur de phase près, se représente sur la sphère de Bloch. Lorsqu’on considère les qubits à un facteur de phase près, on peut donc visualiser la solution de l’équation de Schrödinger sur la sphère de Bloch à l’aide de cette représentation. Nous allons voir que la trajectoire de la solution donne toujours un cercle sur la sphère de Bloch.

Ce résultat est obtenu à l’aide des matrices de Pauli. Ce sont les trois matrices auto-adjointes suivantes :

$$X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad Y = \begin{pmatrix} 0 & i \\ -i & 0 \end{pmatrix}, \quad Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}.$$ Les quatre matrices $I$, $X$, $Y$ et $Z$ sont orthogonales, elles forment donc une base de l’espace des matrices $2\times 2$ complexes. Puisqu’elles sont orthogonales, les coefficients $a$, $b_x$, $b_y$ et $b_z$ tels que $$M = aI + b_x X + b_y Y + b_z Z$$ pour une matrice $M$ donnée, s’obtiennent à l’aide des produits scalaires de $M$ par chacune de ces matrices, et il est alors facile de voir que $a$, $b_x$, $b_y$ et $b_z$ sont des nombres réels lorsque $M$ est une matrice auto-adjointe.

Ainsi, si $M$ est auto-adjointe, on a

$${\mathrm{e}}^{-it M} = {\mathrm{e}}^{-it aI} {\mathrm{e}}^{-it (b_x X + b_y Y + b_z Z)} = {\mathrm{e}}^{-it a} R_{\vec{n}}(2 \lambda t)$$ où l’on note $\lambda = \sqrt{b_x^2+b_y^2+b_z^2}$, $\vec{n} = (n_x, n_y, n_z)$ où $n_x=b_x/\lambda$, $n_y=b_y/\lambda$, $n_z=b_z/\lambda$, et $$R_{\vec{n}}(\theta) = {\mathrm{e}}^{-i \frac{\theta}{2} (n_x X + n_y Y + n_z Z)}.$$

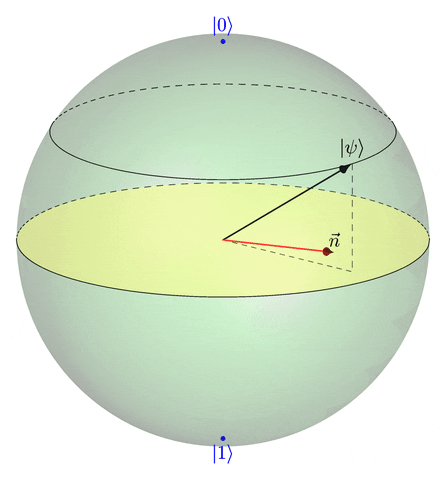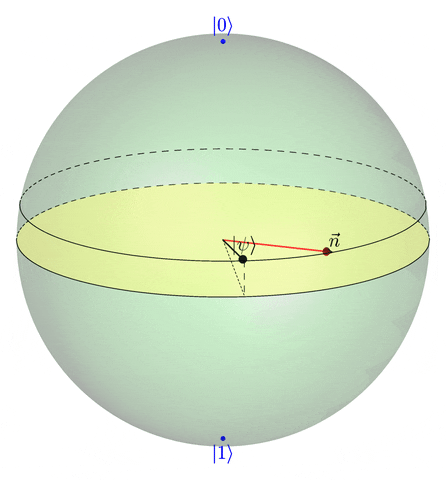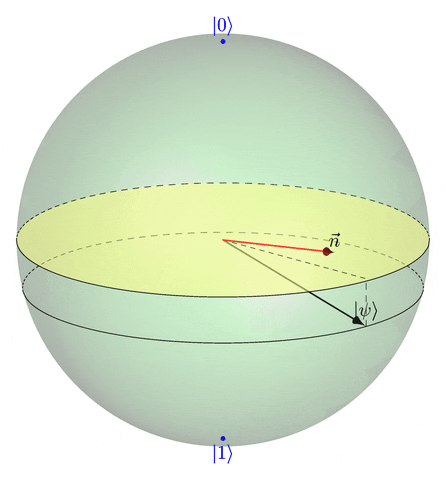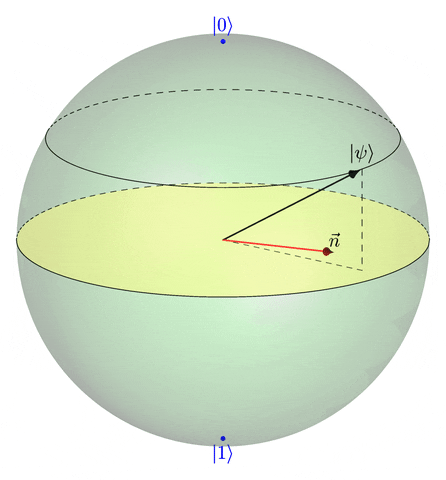
La matrice unitaire $R_{\vec{n}}(\theta)$ est appelée un opérateur de rotation. Ce nom est justifié par le fait suivant : si $\psi \in \mathbb{C}^2$ est un qubit, alors la représentation de $R_{\vec{n}}(\theta) \psi$ sur la sphère de Bloch est l’image de la représentation de $\psi$ sur la sphère de Bloch par la rotation d’angle $\theta$ et d’axe dirigé par le vecteur unitaire $\vec{n}$.

Le résultat annoncé en introduction découle de ce qui précède. Rappelons que la solution de l’équation de Schrödinger

$$\frac{{\mathrm{d}}\psi(t)}{{\mathrm{d}}t} = -{\mathrm{i}}{\mathcal{H}}\psi(t)$$ est $$\psi(t) = U_t\psi(0) \quad \text{où} \; U_t = {\mathrm{e}}^{-{\mathrm{i}}t{\mathcal{H}}}.$$ Donc, si on écrit la décomposition du Hamiltonien ${\cal H}$ dans la base constituée par la matrice $I$ et les matrices de Pauli, $${\cal H} = aI + b_x X + b_y Y + b_z Z$$ on a, avec les notations précédentes, $$U_t = {\mathrm{e}}^{-it a} R_{\vec{n}}(2\lambda t),$$ et donc, à un facteur de phase près, $\psi(t)$ est égal à $$R_{\vec{n}}(2\lambda t) \psi(0).$$ Ainsi, la représentation de $\psi(t)$ sur la sphère de Bloch parcourt un cercle, en tournant autour de l’axe $\vec{n}$ selon un angle qui évolue linéairement en $t$.